-- Load mathjax -->

-- MathJax configuration -->

-- End of mathjax configuration -->

1):

import numpy as np
import matplotlib.pyplot as plt

1차원 이산 확률 변수 1차원 이산 확률 변수의 정의

'추천 관련글,

– 랜덤 변수 X {x1,x2,…}에 대한 가능한 값의 집합

– X가 값 xk를 가질 확률 P(X=xk)=pk(k=1,2,…)

– 확률질량함수(probability function) f(x)=P(X=x)- 불공평한 주사위의 확률분포 – 확률변수 x_set이 가정할 수 있는 값의 집합

2)에서:

x_set = np.array((1, 2, 3, 4, 5, 6))
x_set

꺼짐(2):

array((1, 2, 3, 4, 5, 6))

– x_set에 따른 확률

– 불공평한 주사위에 대한 랜덤 변수

↑

3시에):

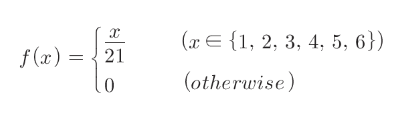
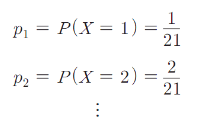
def f(x):
    if x in x_set:
        return x/21
    else:
        return 0

(4)에서:

X = (x_set, f)

5시에):

# 확률 p_k를 구한다.


prob = np.array((f(x_k) for x_k in x_set))
prob

끄기(5):

array((0.04761905, 0.0952381 , 0.14285714, 0.19047619, 0.23809524,
       0.28571429))

(6)에서:

# x_k와 p_k의 대응을 사전식으로 표시
dict(zip(x_set, prob))

밖으로 (6):

{1: 0.047619047619047616,
 2: 0.09523809523809523,
 3: 0.14285714285714285,
 4: 0.19047619047619047,
 5: 0.23809523809523808,
 6: 0.2857142857142857}

(7)에서:

fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111)
ax.bar(x_set,prob)
ax.set_xlabel('value')
ax.set_ylabel('probability')
plt.show()

– 확률의 성질

8시에):

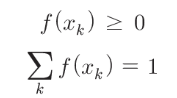
np.all(prob >= 0)

밖으로 (8):

True

– np.all은 모든 요소가 true인 경우에만 true를 반환합니다.

– 확률의 합은 1입니다.

1/21+2/21+3/21+4/21+5/21+6/21=1

(9)에서:

np.sum(prob)

밖으로 (9):

0.9999999999999999

– 누적 분포 함수(distribution function) F(x)

– X가 x보다 작거나 같을 확률을 반환하는 함수

10시):

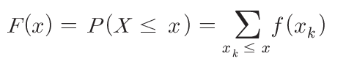
def F(x):
    return np.sum((f(x_k) for x_k in x_set if x_k <= x))

– 눈 확률 3 이하

(11)에서:

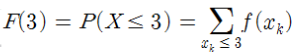
F(3)

끄기(11):

0.2857142857142857

1/21+2/21+3/21 = 0.048+0.095+0.143 = 0.286- 랜덤 변수의 변환

– 랜덤 변수의 변환

– 2X+3, 확률변수 X에 2를 곱하고 3을 더한 것도 확률변수

2X+3이 확률변수 Y라면,

– Y의 확률 분포

(12)에서:

y_set = np.array((2 * x_k+3 for x_k in x_set))
y_set

꺼짐(12):

array(( 5,  7,  9, 11, 13, 15))

(13)에서:

prob = np.array((f(x_k) for x_k in x_set))
dict(zip(y_set, prob))

꺼짐(13):

{5: 0.047619047619047616,
 7: 0.09523809523809523,
 9: 0.14285714285714285,
 11: 0.19047619047619047,
 13: 0.23809523809523808,
 15: 0.2857142857142857}

1차원 이산 랜덤 변수의 인덱스

– 기대값 = 확률변수의 평균

– 랜덤 변수(무제한)를 여러 번 시도하여 얻은 실현 값의 평균

– 무한시도가 없기 때문에 확률의 곱과 확률변수가 취할 수 있는 값의 총합

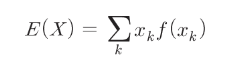
– 부당한 주사위의 기대치

(14)에서:

np.sum((x_k * f(x_k) for x_k in x_set))
# 1x0.048+2X0.095+3X0.143+4X0.190+5X0.238+6X0.286=4.333

꺼짐(14):

4.333333333333333

– 기대값 = 확률변수의 평균

– 100만(10^6) 주사위 굴림의 실현값 평균

(15)에서:

sample = np.random.choice(x_set,1000000,p=prob)
np.mean(sample)

꺼짐(15):

4.333953

– 확률변수 X를 2X+3으로 변환한 후 Y의 기대값

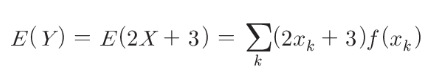
1차원 이산 랜덤 변수의 인덱스

– 기대값 = 확률변수의 평균

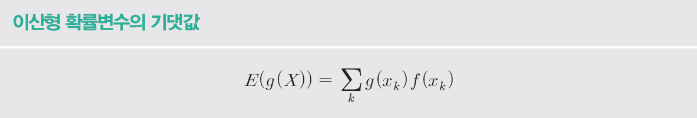
– 예상 값의 함수로 공식을 구현합니다.

– 계수 g는 확률 변수에 대한 변환 함수입니다.

(16)에서:

def E(X, g=lambda x: x):
    x_set, f=X
    return np.sum((g(x_k) * f(x_k) for x_k in x_set))
# g에 아무것도 지정하지 않으면 확률변수 X의 기댓값이 구해짐

(17)에서:

끄기(17):

(array((1, 2, 3, 4, 5, 6)), <function __main__.f(x)>)

– 기대값 = 확률변수의 평균

– 확률변수의 기대값 Y=2X+3

(2X1+3)X0.048+(2X2+3)X0.095+…(2X6+3)X0.286 = 11.667

(18)에서:

E(X, g=lambda x:2*x+3)

끄기(18):

11.666666666666664

참고: Lambda 함수(익명 함수)

– 값을 반환하는 간단한 단일 명령문 함수

– 더 적은 코드와 더 간결한

def short_function(x): return x*2 equiv_anon = lambda x: x*2

def apply_to_list(some_list, f): 
	return ((f(x) for x in some_list) 

ints = (4, 0, 1, 5, 6) 
apply_to_list(ints, lambda x: x*2) 

(x*2 for x in ints)

– 기대값 = 확률변수의 평균

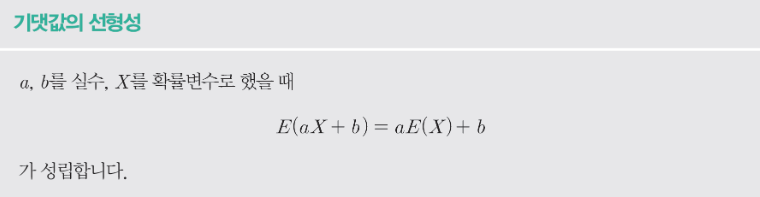
– E(2X+3) = 2E(X)+3

19에서):

2 * E(X)+3

꺼짐(19):

11.666666666666666

– 혼란

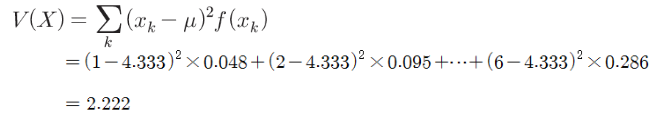
– 부당한 주사위 던지기

20에서):

mean = E(X)
np.sum(((x_k-mean)**2 * f(x_k) for x_k in x_set))

꺼짐(20):

2.2222222222222223

– 확률변수 Y=2X+3의 분산

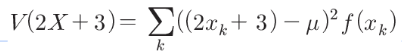
– 혼란

– 분산의 함수로서 이산 확률 변수의 분산 방정식 구현

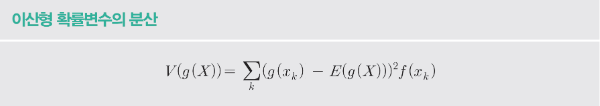
– 계수 g는 확률 변수에 대한 변환 함수입니다.

(21)에서:

def V(X, g=lambda x: x):
    x_set, f=X
    mean = E(X,g)
    return np.sum(((g(x_k)-mean) ** 2 * f(x_k) for x_k in x_set))

(22)에서:

V(X)

꺼짐(22):

2.2222222222222223

– 확률변수 Y=2X+3의 분산

(23)에서:

V(X, lambda x: 2*x+3)

꺼짐(23):

8.88888888888889

– 혼란

– V(2X+3) = 2^2V(X)

(24)에서:

2**2 * V(X)

꺼짐(24):

8.88888888888889

2D 이산 랜덤 변수란 무엇입니까?

– 결합확률분포(2개의 1차원 확률분포를 동시에 처리(X,Y), 확률은 X와 Y가 각각 가정할 수 있는 값의 조합으로 정의) – 확률변수 X는 xi, 확률변수 Y는 yi를 취할 확률

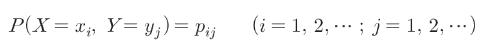
– 랜덤 변수(X, Y)의 동시 이동을 고려한 분포.

– Unfair Dice A and B – X가 A와 B의 눈에, Y가 A의 눈에 더해지는 2차원 확률 분포

– 공동 확률 함수

– P(X=x, Y=y) = fxy(x,y)

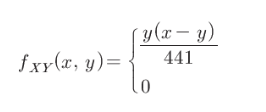
– 확률의 성질

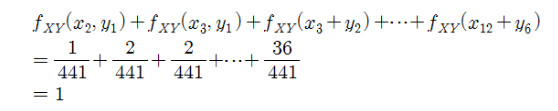
– X와 Y의 가능한 값 집합

(25)에서:

x_set = np.arange(2, 13)
y_set = np.arange(1, 7)

– 공동 확률 함수

(26)에서:

def f_XY(x, y):
    if 1<= y <= 6 and 1 <= x-y <=6:
        return y * (x-y)/441
    else:
        return 0

(27)에서:

XY = (x_set, y_set, f_XY)

(28)에서:

XY

꺼짐(28):

(array(( 2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12)),
 array((1, 2, 3, 4, 5, 6)),
 <function __main__.f_XY(x, y)>)

– 확률 분포 히트맵

(29)에서:

prob = np.array(((f_XY(x_i,y_j) for y_j in y_set)
                for x_i in x_set))

fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111)

c = ax.pcolor(prob)
ax.set_xticks(np.arange(prob.shape(1)) + 0.5, minor=False)
ax.set_yticks(np.arange(prob.shape(0)) + 0.5, minor=False)
ax.set_xticklabels(np.arange(1, 7), minor=False)
ax.set_yticklabels(np.arange(2, 13), minor=False)
# y축을 내림차순의 숫자가 되게 하여, 위 아래를 역전시킨다.


ax.invert_yaxis()
# x축 눈금을 그래프 위쪽에 표시
ax.xaxis.tick_top()
fig.colorbar(c, ax=ax)
plt.show()

– 확률의 성질

(30)에서:

np.all(prob>=0)

꺼짐(30):

True

(31)에서:

np.sum(prob)

끄기(31):

1.0

– 한계 확률 분포

– 확률변수(X,Y)가 동시에 결합확률분포로 정의되는데, 확률변수 X의 확률함수 fx(x)를 알고 싶다.

– fXY에 Y의 가능한 모든 값을 대입한 후 모두 더하기

(32)에서:

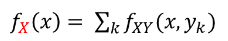
def f_X(x):
    return np.sum((f_XY(x, y_k) for y_k in y_set))

(33)에서:

def f_Y(y):
    return np.sum((f_XY(x_k, y) for x_k in x_set))

(34)에서:

X = (x_set, f_X)
Y = (y_set, f_Y)

한계 분배

(35)에서:

prob_x = np.array((f_X(x_k) for x_k in x_set))
prob_y = np.array((f_Y(y_k) for y_k in y_set))

fig = plt.figure(figsize=(12, 4))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
ax1.bar(x_set, prob_x)
ax1.set_title('X_marginal probability distribution')
ax1.set_xlabel('X_value')
ax1.set_ylabel('probability')
ax1.set_xticks(x_set)

ax2.bar(y_set, prob_y)
ax2.set_title('Y_marginal probability distribution')
ax2.set_xlabel('Y_value')
ax2.set_ylabel('probability')

plt.show()

2차원 이산 랜덤 변수의 인덱스

– 기대값

(36)에서:

np.sum((x_i * f_XY(x_i, y_j) for x_i in x_set for y_j in y_set))

꺼짐(36):

8.666666666666666

– 기대값에 따라 구현

(37)에서:

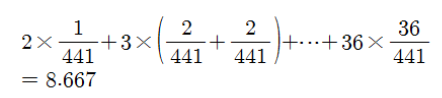
def E(XY, g):
    x_set, y_set, f_XY = XY
    return np.sum((g(x_i, y_j) * f_XY(x_i, y_j)
                  for x_i in x_set for y_j in y_set))

– X와 Y의 기대값

(38)에서:

mean_X = E(XY, lambda x, y:x)
mean_X

끄기(38):

8.666666666666666

(39)에서:

mean_Y = E(XY, lambda x, y:y)
mean_Y

(39)에서:

4.333333333333333

(40)에서:

a, b= 2, 3

(41)에서:

E(XY, lambda x, y: a*x + b*y)
# 2X8.667+3X4.333 = 30.333

끄기(41):

30.333333333333332

(42)에서:

a * mean_X + b * mean_Y

끄기(42):

30.333333333333332

– 혼란

– X의 분산은 X에 대한 제곱 분산의 기대값입니다.

(43)에서:

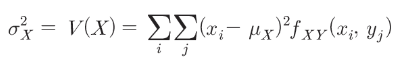
np.sum(((x_i-mean_X)**2 * f_XY(x_i, y_j)
       for x_i in x_set for y_j in y_set))

꺼짐(43):

4.444444444444444

– X와 Y의 함수 g(X,Y)의 분산

(44)에서:

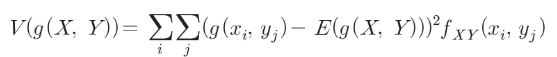
def V(XY, g):
    x_set, y_set, f_XY = XY
    mean = E(XY, g)
    return np.sum(((g(x_i, y_j)-mean)**2 * f_XY(x_i, y_j)
                  for x_i in x_set for y_j in y_set))

– X와 Y의 분산

(45)에서:

var_X = V(XY, g=lambda x, y: x)
var_X

끄기(45):

4.444444444444444

(46)에서:

var_Y = V(XY, g=lambda x, y: y)
var_Y

꺼짐(46):

2.2222222222222223

– 공분산

– 두 확률변수 X,Y의 상관관계

(47)에서:

def Cov(XY):
    x_set, y_set, f_XY = XY
    mean_X = E(XY, lambda x, y: x)
    mean_Y = E(XY, lambda x, y: y)
    return np.sum(((x_i-mean_X) * (y_j-mean_Y) * f_XY(x_i, y_j)
                  for x_i in x_set for y_j in y_set))

(48)에서:

cov_xy = Cov(XY)
cov_xy

끄기(48):

2.222222222222222

(49)에서:

V(XY, lambda x, y: a*x + b*y)

꺼짐(49):

64.44444444444444

(50)에서:

a**2 * var_X + b**2 * var_Y + 2*a*b * cov_xy

꺼짐(50):

64.44444444444443

– 상관 계수

(51)에서:

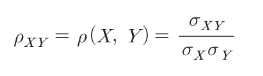
cov_xy / np.sqrt(var_X * var_Y)

(51)에서:

0.7071067811865474